前回の記事と前々回の記事では,
- 等差数列の和
- 等比数列の和
を考えました.その際,和を
と書き並べて表すのは少々面倒です.
この程度ならまだ少し面倒なくらいですが,もっと複雑になると大変ですね.
そこで,数列の和を短く表す記号としてシグマ記号$\sum$があります.
この記事では,
- シグマ記号$\sum$の定義
- シグマ記号$\sum$の具体例
- シグマ記号$\sum$の基本性質
を順に説明します.
「数列」の一連の記事
シグマ記号$\sum$
まずはシグマ記号$\sum$の定義と具体例をみてみましょう.
シグマ記号の定義
正の整数$n$に対して,数列$\{a_n\}$の初項$a_1$から第$n$項$a_n$までの全ての和$a_1+a_2+\dots+a_n$を$\sum\limits_{k=1}^{n}a_k$と表す.すなわち,
である.
和は英語で“sum”であり,$\Sigma$は“S”に相当するギリシャ文字の大文字です.また,$\Sigma$の小文字は$\sigma$です.
要するに$\sum\limits_{k={\color{magenta}1}}^{\color{blue}n}$は「$k$に$\color{magenta}1$から$\color{blue}n$までの整数を代入したものを足せ」という意味の記号というわけですね.
そもそもシグマ記号はまだ紙が貴重だった時代に省スペースのために考案されたのが起源で,シグマ記号を使うことによって式がスッキリ書けるというメリットがあります.
また,初項$a_1$からではなく第$m$項からの和を考えたいときは同様に次のように表します.
正の整数$m$, $n$ ($m\le n$)に対して,数列$\{a_n\}$の第$m$項$a_m$から第$n$項$a_n$までの全ての和$a_m+a_{m+1}+\dots+a_n$を$\sum\limits_{k=m}^{n}a_k$と表す.すなわち,
である.
$2\le m\le n$なら
ということですね.
シグマ記号の具体例
具体的に考えてみましょう.
次の和を書き並べて表せ.
(1) $\sum\limits_{k=1}^{5}$は「$k$に$1$から$5$までの整数を代入して足し合わせる」という意味だから,
(2) $\sum\limits_{k=1}^{3}$は「$k$に$1$から$3$までの整数を代入して足し合わせる」という意味だから,
(3) $\sum\limits_{k=7}^{10}$は「$k$に$7$から$10$までの整数を代入して足し合わせる」という意味だから,
(4) $\sum\limits_{k=1}^{4}$は「$k$に$1$から$4$までの整数を代入して足し合わせる」という意味だから,
最後の例について,一般に定数$a$に対して$\sum\limits_{k=1}^{n}a$は「$k$を代入してもいつでも$a$」と考えて,$a$を$n$回足し合わせることに注意してください.
シグマ記号の基本性質
次にシグマ記号$\sum$の基本性質を説明します.
基本性質
次の性質はシグマ記号$\sum$の計算をする上で大切です.
数列$\{a_n\}$, $\{b_n\}$と定数$p$, $q$に対して,
が成り立つ.
つまり,和はバラバラにでき,定数倍は$\sum$の外に出せるわけですね.
実際に書き並べて変形することで
と
が得られる.
この2つの等式を併せると次が成り立ちますね.
数列$\{a_n\}$, $\{b_n\}$と実数$p$, $q$に対して,
が成り立つ.
高校数学では知らなくても問題ありませんが,$\sum$のように和をバラバラにでき,定数倍を外に出せる性質を線形性といいます.
基本性質の具体例
次の和を$n$を用いて表せ.
求める和は
とできるから,$\sum\limits_{k=1}^{n}k$と$\sum\limits_{k=1}^{n}2^k$を求めれば良い.
$\sum\limits_{k=1}^{n}k$は$1+2+3+\dots+n$で初項$1$,公差$1$の等差数列の和だから
である.また,$\sum\limits_{k=1}^{n}2^k$は$2+2^2+2^3+\dots+2^n$で初項$2$,公比$2$の等比数列の和だから
である.
以上より,
を得る.
なお,途中で用いた等差数列の和の公式と等比数列の和の公式については以下の記事を参照してください.
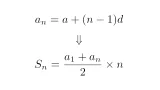
等差数列の和の公式を直感的に理解する方法
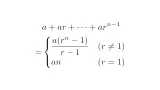
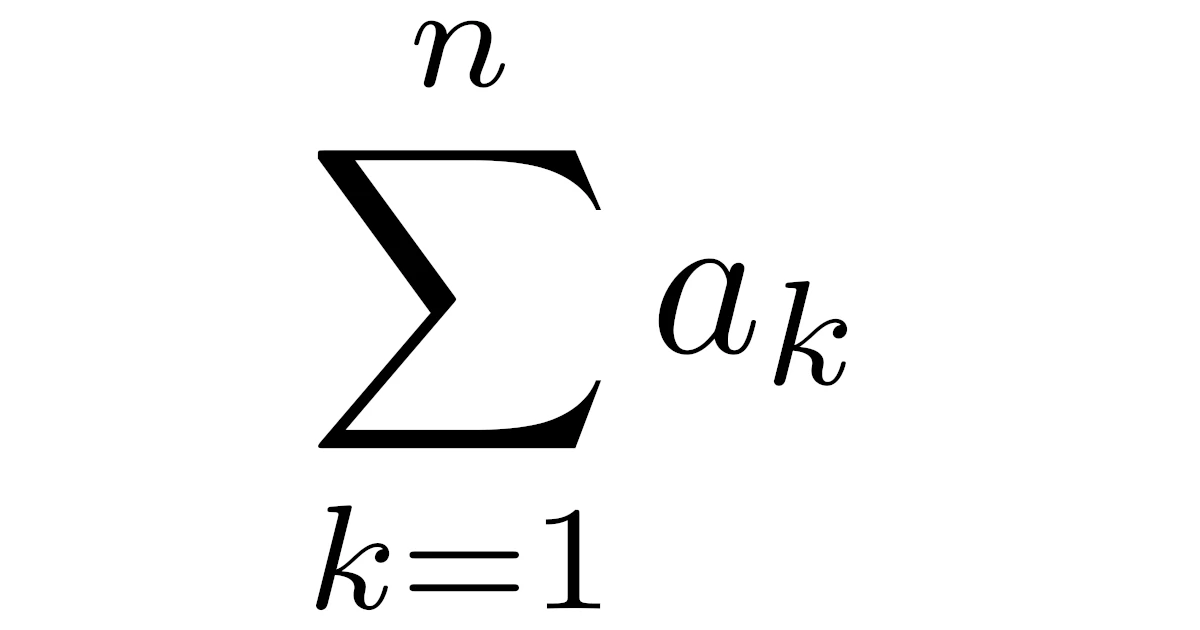
コメント