数列２<br>等差数列の和の公式を直感的に理解する方法

前回の記事でも説明したように，数列の中でも

等差数列
等比数列

は考えやすく，一般項も簡単に求められるのでした．

数列$\{a_n\}$に対して，初項$a_1$から第$n$項$a_n$までの和

$\begin{align*}a_1+a_2+a_3+\dots+a_{n-1}+a_n\end{align*}$

を考えることはよくあり，等差数列と等比数列のこの和も簡単に求めることができます．

等比数列の和については次の記事に譲るとし，この記事では

等差数列の和の公式
等差数列の和の直感的な理解
等差数列の和の具体例
等差数列の和の公式の導出

を順に説明します．

「数列」の一連の記事

数列の基礎

漸化式

等差数列の和
1. 具体例１
2. 具体例２
等差数列の和の公式の導出

等差数列の和

早速，等差数列の和の公式を紹介します．

初項$a$，公差$d$の等差数列の初項から第$n$項までの和$S_n$は

$\begin{align*}S_n=\frac{n\{2a+(n-1)d\}}{2}\end{align*}$

である．

直感的には等差数列$\{a_n\}$に対して$a_1,a_2,\dots,a_n$は等間隔なので，全体の平均と$a_1,a_n$の平均が等しいです．

よって，全体の和$S_n$は$a_1,a_n$の平均の$n$倍に等しく，

$\begin{align*}S_n=&\frac{a_1+a_n}{2}\times n \\=&\frac{a+\{a+(n-1)d\}}{2}\times n \\=&\frac{n\{2a+(n-1)d\}}{2}\end{align*}$

と分かりますね．

分子の$2a+(n-1)d$が

初項$a_1=a$
第$n$項$a_n=a+(n-1)d$

の和だという認識をもてれば，間違えることはありませんね．

具体例１

初項$1$，公差$1$の等差数列$1,\ 2,\ 3,\ 4,\dots$の初項から第$n$項までの和を$n$で表せ．

上の公式の$a=1$, $d=1$の場合なので，

$\begin{align*}1+2+3+\dots+n=\frac{n(n+1)}{2}\end{align*}$

である．

直感的には初項の$1$から第$n$項の$n$までの平均が$\dfrac{n+1}{2}$で，全部で$n$項足し合わせているから

$\begin{align*}n\times\frac{n+1}{2}=\frac{n(n+1)}{2}\end{align*}$

と理解できますね．

具体例２

等差数列$3,\ 7,\ 11,\ 15,\ 19,\dots$の初項から第$50$項までの和を求めよ．

等差数列$3,\ 7,\ 11,\ 15,\ 19,\ \dots$は初項$3$，公差$4$の等差数列だから上の公式の$a=3$, $d=4$の場合である．

よって，この数列の初項から第$50$項までの和は

$\begin{align*}&\frac{50(2\times3+(50-1)\times4)}{2} \\=&50(3+49\times2) \\=&150+49\times100 =5050\end{align*}$

である．

直感的には初項の$3$から第$50$項の$3+49\times4$までの平均が$\frac{3+(3+49\times4}{2}$で，全部で$50$項足し合わせているから

$\begin{align*}50\times\frac{3+(3+49\times4}{2}\end{align*}$

と理解できますね．

等差数列の和の公式の導出

先ほどの直感的な公式の導出と本質的には同様ですが，もう少しきちんと導出しておきましょう．

（再掲）初項$a$，公差$d$の等差数列の初項から第$n$項までの和$S_n$は

$\begin{align*}S_n=\frac{n\{2a+(n-1)d\}}{2}\end{align*}$

である．

初項$a$，公差$d$の等差数列を$\{a_n\}$とすると，初項$a_1$から第$n$項$a_n$までの和$S_n$は

$\begin{align*}S_n=&a_1+a_2+a_3+\dots+a_n \\=&a+(a+d)+(a+2d)+\dots+\{a+(n-1)d\}\end{align*}$

である．また，これとは逆順に第$n$項$a_n$から初項$a_1$まで足すと考えれば，

$\begin{align*}S_n=\{a+(n-1)d\}+\{a+(n-2)d\}+\{a+(n-3)d\}+\dots+a\end{align*}$

でもある．よって，この２式の辺々を足せば，

$\begin{align*}\begin{matrix}&S_n&=&a&+&\dots&+&\{a+(n-1)d\}\\ -)&S_n&=&\{a+(n-1)d\}&+&\dots&+&a\\ \hline &2S_n&=&2a+(n-1)d&+&\dots&+&2a+(n-1)d\end{matrix}\end{align*}$

となる．

このとき，右辺は$2a+(n-1)d$が$n$個足されているので，

$\begin{align*}&2S_n=n\{2a+(n-1)d\} \\\iff&S_n=\dfrac{n\{2a+(n-1)d\}}{2}\end{align*}$

を得る．

いまの導出は$a$, $d$が正の整数の場合は次のようにブロックの個数を考えることで理解できます．

$S_n$は以下のブロックの総数に等しいですね．

$S_n$の和の順を逆にしたものと足し合わせたものは，ブロックを逆さまにして

と併せたブロックの個数は$n\times\{2a+(n-1)d\}$です．よって，求める$S_n$はこの半分で

$\begin{align*}\frac{n\{2a+(n-1)d\}}{2}\end{align*}$

となりますね．

数列２
等差数列の和の公式を直感的に理解する方法

等差数列の和

具体例１

具体例２

等差数列の和の公式の導出

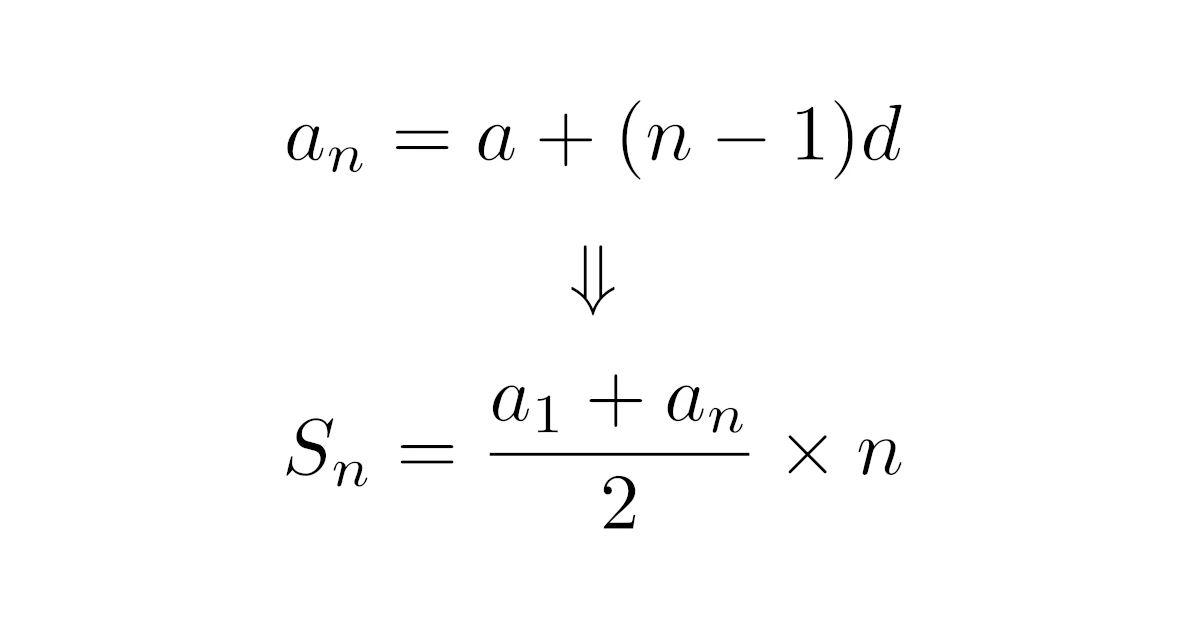
コメント