数学IIで2次方程式を解くために少し登場した複素数ですが,数学IIIではこの複素数が1つの大きな分野として登場します.
実数は数直線上に図示して「見る」ことができるように,複素数も図示して「見る」ことができます.
そのため,一度イメージが分かってしまえば複素数も直感的に捉えることができます.
複素数の図示については次の記事で説明しています.
複素数は現代科学ではなくてはならないものであり,例えば電子機器は複素数の理論なしでは作ることができません.
このように,複素数は数学のみならず大学以降では物理など多分野でも非常に重要な役割を役割を担っています.
この記事では
- そもそも複素数とは何か?
- 複素数の基礎知識
を順に説明します.
「複素数」の一連の記事
複素数
複素数がどういうものかを説明するためには,虚数単位$i$を説明する必要があります.
虚数単位の定義
例えば,
のように,我々がこれまで触れてきた実数は2乗すると$0$以上の実数となるのでした.
それでは,$x$の2次方程式$x^2=-1$の解はどのように考えれば良いでしょうか?
2乗して負の数$-1$になる実数はありませんから,2次方程式$x^2=-1$が実数解をもたないことは分かります.
そこで,次のように虚数単位なるものを定義します.
$x$の方程式$x^2=-1$の解の1つを虚数単位 (imaginary unit)といい,$i$で表す.
要するに$i^2=-1$となるような数$i$を新しく考えてやろうというわけです.
2次方程式と虚数単位
最初は虚数単位$i$に気持ち悪い印象をもってしまうかも知れませんが,$i^2=-1$となる虚数単位$i$を定義すると良いことがいくつかあります.
たとえば,実数の範囲で解をもたなかった$x$の2次方程式$x^2=-1$は次のように虚数単位を用いて解くことができます.
$x$の2次方程式$x^2=-1$を解け.
$-1=i^2$だから,
と解ける.
この記事の後で説明するように,虚数単位$i$は普通の文字と同じように計算します.
実数の範囲で解くことができなかった方程式の解も表せるようになるのは,虚数単位を定義する大きなメリットの1つです.
複素数
この虚数単位を用いて複素数を次のように定義します.
実数$a$, $b$を用いて,
と表される数$z$を複素数(complex number)といい,$a$を$z$の実数部分(実部,real part),$b$を$z$の虚数部分(虚部,imaginary part)という.
ここで,$a$, $b$は$0$であってもよいことに注意しましょう.つまり,
などは全て複素数です.実数も複素数の一種であることに注意しましょう.
複素数$z=a+bi$($a$, $b$は実数)を考える.$b\neq0$のとき,この複素数$z$を虚数(imaginary number)という.さらに$a=0$であれば,$z$を純虚数(pure imaginary number)という.
つまり,虚部が$0$でない複素数を虚数といい,そのもとで実部が$0$であるような虚数を純虚数というわけですね.たとえば,
などは全て虚数で,このうちでは$3i$のみが純虚数です.
さて,実数は虚部が$0$の複素数ですから,次のことが分かりますね.
複素数は実数または虚数である.
つまり,$i$が残っていなければ実数で,$i$が残っていれば虚数というわけですね.
このように,虚数と複素数は別物なので,はっきり区別して理解しておいてください.
複素数の基礎知識
複素数を定義したので,次は複素数の基礎知識を整理していきましょう.
複素数の相等
さて,2つの複素数$z$, $w$があるとき,この2つが等しいとは以下のように定義します.
2つの複素数$z=a+bi$, $w=c+di$ ($a$, $b$, $c$, $d$は実数)に対して,$a=c$かつ$b=d$が成り立つとき,$z$と$w$は等しいといい$z=w$と表す.
すなわち,複素数$z$, $w$に対して,これらの実部同士,虚部同士がそれぞれ等しいとき$z=w$というわけですね.
たとえば,実数$a$, $b$に対して,複素数$z=2+3ai$, $w=3b-6i$が$z=w$を満たせば,
となるわけですね.
複素数の四則演算
複素数の四則計算は$i^2=-1$であること以外は普通の文字計算と同様に計算します.
たとえば,$z=2+3i$, $w=3-2i$に対して,
となります.
割り算は分母の有理化と同じように$3+2i$で$2i$の正負を変えた$3-2i$をかけることで,分母から虚数単位が消えています.
この計算はよく現れるので覚えておいてください.
普通の文字式の計算と同じなので,和と積に関して
と和と積に関して交換法則が成り立ちますね.また,実数の場合と同様に
- 自然数$n$に対して$z^{n}$は$n$個の$z$の積
- $z^{0}=1$
- $z^{-n}$は$z^{n}$の逆数
と定めます.
このように,$i$が普通の文字のように計算できることから,2次方程式も実数のときと同じように解くことができます.
$x$の2次方程式$x^2-2x+2=0$を解け.
共役複素数
最後に共役複素数を定義しましょう.
複素数$z=a+bi$ ($a$, $b$は実数)に対して,複素数$a-bi$を$z$の共役複素数といい,$\overline{z}$で表す.
要するに虚部だけに$-1$をかけた複素数を共役複素数というわけですね.
たとえば,$z=1+3i$の共役複素数$\overline{z}$は$\overline{z}=1-3i$です.
複素数の実部と虚部
複素数$z$が与えられたとき,$z$と共役複素数$\overline{z}$を用いて$z$の実部と虚部を表すことができます.
複素数$z=a+bi$ ($a$, $b$は実数)に対して,
が成り立つ.
$z=a+bi$から$\overline{z}=a-bi$なので,
となるから,
が成り立つ.
共役複素数と四則演算
共役複素数は四則演算に関してバラバラにできます.すなわち,以下が成り立ちます.
複素数$z$, $w$に対して,
が成り立つ.
$z=a+bi$, $w=c+di$ ($a$, $b$, $c$, $d$は実数)とすると,$\overline{z}=a-bi$, $\overline{w}=c-di$なので,
が成り立つことが分かります.
この定理から,任意の複素数$z_1,z_2,\dots,z_n$に対して,
が成り立ち,任意の自然数$n$と複素数$z$に対して,
が成り立つことが分かりますね.
厳密には数学的帰納法から証明できますね.
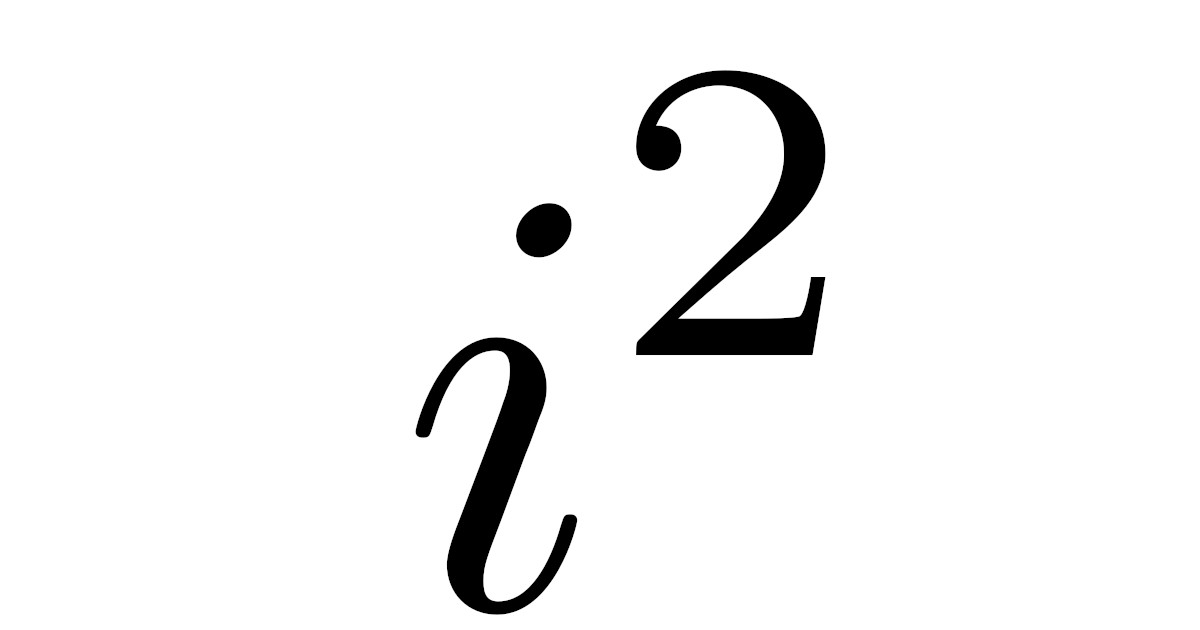
コメント