次の問題はどのように考えれば良いでしょうか?
$xy$平面上の$y=2x^{3}$のグラフ上の点$(-1,-2)$での接線$\ell$の方程式を求めよ.
数学Iで学ぶように,2次関数の接線は判別式$D$を利用する方法がありましたが,この問題は3次関数なので判別式を用いて考えることはできません.
2次式でない多項式に対しては,微分係数というものを考えることで接線の方程式を考えることができます.
この記事では
- 接線の傾きと微分係数
- 微分係数の定義
- 微分係数の具体例(接線の方程式の求め方)
を順に説明します.
「微分法」の一連の記事
接線の傾きと微分係数
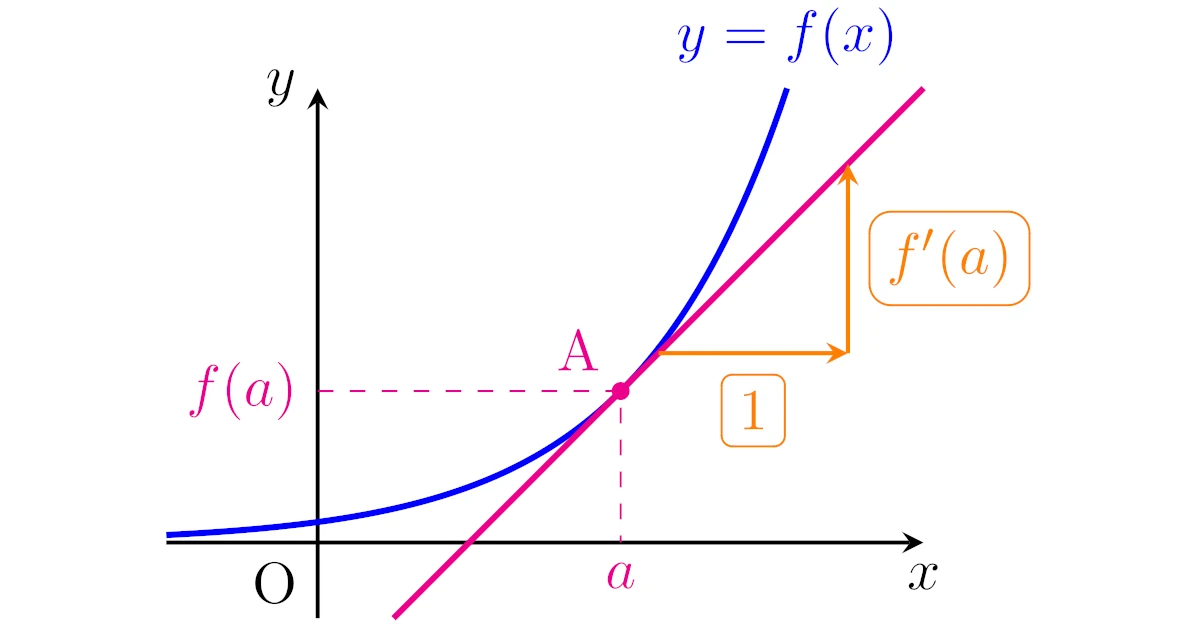
$xy$平面上の$y=f(x)$のグラフ上に点$\mrm{A}(a,f(a))$を考えます.
このときの点$\mrm{A}$での$y=f(x)$のグラフの接線$\ell$の方程式の求め方を考えましょう.
直線の方程式の求め方
$xy$平面上の直線の方程式を求める次の公式は当たり前にしておきましょう.
$xy$平面上の傾き$m$で点$(a,b)$を通る直線の方程式は$y=m(x-a)+b$である.
つまり,直線の方程式を求めるためには,通る点と傾きさえ分かれば良いというわけですね.
$y=f(x)$の点$\mrm{A}(a,f(a))$での接線$\ell$は点$\mrm{A}(a,f(a))$を通りますから,あとは傾きさえ分かれば接線$\ell$の方程式が求まりますね.
接線の傾きの考え方
それでは$y=f(x)$の点$\mrm{A}(a,f(a))$での接線$\ell$の傾きの求め方を考えましょう.
まず,点$\mrm{A}(a,f(a))$と異なる$y=f(x)$上の点$\mrm{B}(b,f(b))$をとり,直線$\mrm{AB}$を考えます.
このとき,直線$\mrm{AB}$の傾きは$\dfrac{f(b)-f(a)}{b-a}$ですね.これを$a$から$b$までの$f$の平均変化率といいます.
ここで点$\mrm{B}(b,f(b))$の$x$座標$b$を$a$に近付けると,直線$\mrm{AB}$は接線$\ell$に近付いていくことが見て取れますね.
このため,平均変化率$\dfrac{f(b)-f(a)}{b-a}$で$b$を$a$に近付ければ,直線$\mrm{AB}$の傾きは直線$\ell$の点$\mrm{A}$での接線の傾きに近付いていくと直感的に言えそうです.
微分係数と接線の方程式
いま考えたことから微分係数を定義して,接線の方程式の考え方を解説します.
微分係数の定義
いまの「$b$を$a$に近付ける」というのは数学の言葉では$b\to a$の極限といい,いまの場合
と表します.この平均変化率$\dfrac{f(b)-f(a)}{b-a}$の$b\to a$での極限を点$a$での$f$の微分係数といいます.
関数$f$と異なる実数$a$, $b$に対して,$a$から$b$までの$f$の平均変化率$\frac{f(b)-f(a)}{b-a}$の$b\to a$の極限
が存在するとき,この極限を関数$f$の$a$における微分係数といい$f'(a)$と表す.また,$f$は$a$で微分可能であるという.
極限$\lim\limits_{b\to a}\dfrac{f(b)-f(a)}{b-a}$が存在しないこともありますが,数学IIの微分で主に扱う多項式$f(x)$は任意の$a$で微分可能です.つまり,多項式$f(x)$の微分係数はいつでも存在すると思っていて問題ありません.
接線の方程式
以上から,$xy$平面上の$y=f(x)$のグラフの接線の方程式は次で得られますね.
実数$a$と関数$f$に対して,$f$は$a$で微分可能であるとする.このとき,$xy$平面上の$y=f(x)$のグラフの$a$での接線は
である.
大切なことは$xy$平面上の$y=f(x)$のグラフの$x=a$での接線の傾きが微分係数$f'(a)$であるということですね.
接線の方程式の具体例
それでは$xy$平面上の接線の方程式を具体的に求めてみましょう.
具体例1
$xy$平面上の$y=x^2$のグラフの$x=1$での接線の方程式を求めよ.
$f(x)=x^{2}$とする.$f(1)=1$だから$y=f(x)$の$x=1$での接線は点$(1,1)$を通る.$f$の$1$での微分係数$f'(1)$は
だから,接線の傾きは$2$である.よって,求める接線の方程式は
となる.
直線の方程式は「通る点」と「傾き」が分かれば求められるということを意識してください.
具体例2
次の具体例も具体例1と同様に考えられます.
$xy$平面上の$y=2x^{3}$のグラフの$x=-1$での接線の方程式を求めよ.
$f(x)=2x^{3}$とする.$f(-1)=-2$だから$y=f(x)$の$x=-1$での接線は点$(-1,-2)$を通る.$f$の$-1$での微分係数$f'(-1)$は
だから,接線の傾きは$6$である.よって,求める接線の方程式は
となる.
補足(「接線」とはそもそも何か?)
最後に接線について少し厳密な話をしますが,高校数学ではここまで知っている必要はないので,以上で納得した人は読まなくても構いません.
ここで考えたいことは「$xy$平面上の$y=f(x)$のグラフの「接線」はどのように定義されるのか?」です.
関数$f$が2次関数の場合は「$y=g(x)$と$y=ax+b$から$y$を消去してできる方程式について,判別式が$0$となるとき$y=ax+b$を$y=f(x)$の接線という」と定義することはできますが,$f$が2次関数でない場合はどうでしょうか?
$f$が2次関数でなければいまのように判別式は考えられませんから,同様に定義することはできません.
実は厳密には$xy$平面上の$y=f(x)$のグラフの$x=a$での接線は次のように定義されます.
実数$a$と関数$f$に対して,$f$は$a$で微分可能であるとする.このとき,$xy$平面上の点$\mrm{A}(a,f(a))$を通り,傾き$f'(a)$の直線$\ell$を$y=f(x)$のグラフの$x=a$における接線という.また,点$\mrm{A}$を接線$\ell$の接点という.
つまり,高校範囲では接線がどういうものか直感的に扱われているので,先ほど説明したように「点$(a,f(a))$を通り,傾き$f'(a)$の直線が接線だから,接線の方程式は$y=f'(a)(x-a)+f(a)$である」という説明になるのですが,厳密には逆でこれが定義となっているわけですね.
コメント