等差数列の和の公式と等比数列の和の公式は簡単に求められる数列の和としてよく知られています.
この他に和がよく知られているものとしては
- 1乗和$1+2+3+\dots+n$
- 2乗和$1^2+2^2+3^2+\dots+n^2$
- 3乗和$1^3+2^3+3^3+\dots+n^3$
があります.この記事では
- 1乗和・2乗和・3乗和の公式
- 1乗和・2乗和・3乗和の公式の証明
- 4乗和・5乗和・……の公式の求め方
を順に説明します.
「数列」の一連の記事
1乗和・2乗和・3乗和の公式
まずは公式を紹介して,具体例で使い方をみましょう.
公式
$1$から$n$までの整数の1乗和・2乗和・3乗和は次のようになります.
等式
が成り立つ.
「1乗和」という表現は少し気持ち悪いですが,「2乗和」,「3乗和」との対応で「1乗和」という表現を使うことにします.
シグマ記号$\sum$を用いて
と書いても同じことですね.
のちに説明するように1乗和はすぐに導けますが,2乗和・3乗和の導出は時間がかかってしまうため,2乗和・3乗和の公式は覚えてしまうのがよいでしょう.
とはいえ,3乗和はたまたま「1乗和の2乗」になっているので覚えやすいので,結局ほとんど2乗和だけを覚えれば十分ですね.
具体例
次の和を求めよ.
- $1+2+\dots+100$
- $1^2+2^2+\dots+10^2$
- $1^3+2^3+\dots+8^3$
(1) 1乗和の公式で$n=100$の場合なので,
である.
(2) 2乗和の公式で$n=10$の場合なので,
である.
(3) 3乗和の公式で$n=8$の場合なので,
である.
公式の導出
それでは$1$から$n$までの整数の1乗和・2乗和・3乗和の公式を導出しましょう.
この2乗和・3乗和の導出法は次の記事で説明する階差数列の公式の導出と似た方法なので,この導出法も覚えておきたいところです.
1乗和の公式の導出
1乗和の公式では
- 等差数列の和の公式を用いた導出
- 直感的な導出
の2つの方法を紹介します.
(再掲)等式
が成り立つ.
等差数列の和の公式を用いた導出
初項$a$,公差$d$の等差数列の初項から第$n$項までの和は
であったことを思い出しましょう.この公式は覚えていなくてもすぐに導けることを以前の記事で説明しました.
この公式から次のように導くことができますね.
和$1+2+3+\dots+n$は初項$1$,公差$1$の等差数列の初項から第$n$項までの和である.
よって,上の等差数列の和の公式に$(a,d)=(1,1)$を代入して
と1乗和の公式が得られる.
直感的な導出
ただ証明するだけならいまの方法で十分ですが,次の直感的な導出法も知っておくと理解が深まります.
1個のブロック,2個のブロック,3個のブロック,4個のブロック,……を以下のように並べていきましょう.
これを$n$まで続けると,$1+2+\dots+n$のブロックが下図のように並びます.
このブロックと同じものを逆さまにして連結させると,数のように$n\times(n+1)$の長方形になります.
この長方形は$n(n+1)$個のブロックで構成されており,元の$1+2+3+\dots+n$はその半分なので,
が得られました.
この直感的な考え方は本質的に等差数列の和の公式の導出と同じ考え方です.
2乗和の公式の導出
(再掲)等式
が成り立つ.
任意の正の整数$k$に対して,等式
が成り立つ(単純に左辺を展開すれば得られる)から,この等式の$k$に$k=1,2,\dots,n$を代入したものをすべてを足し合わせると,
となる(左辺はほとんどがマイナスとプラスで打ち消し合って$n^3$と$0^3$だけが残る).
こうして得られた等式
の右辺の第2項の$\sum\limits_{k=1}^{n}k$は1乗和$\dfrac{n(n+1)}{2}$なので,
となる.これを整理すると,
を得る.
2乗和の公式の導出のポイントとなったのは等式$k^3-(k-1)^3=3k^2-3k+1$ですね.
$k=1,2,\dots,n$を代入したものを足し合わせると,左辺がプラスマイナスでほとんど打ち消し合うのがミソですね.
3乗和の公式の導出
(再掲)等式
が成り立つ.
証明の流れは2乗和の公式と同様です.
任意の正の整数$k$に対して,等式
が成り立つから,この等式の$k$に$k=1,2,\dots,n$を代入したものをすべてを足し合わせると,
となる.こうして得られた等式
の右辺の第2項の$\sum\limits_{k=1}^{n}k^2$は2乗和$\dfrac{n(n+1)(2n+1)}{6}$,第3項の$\sum\limits_{k=1}^{n}k^2$は1乗和$\dfrac{n(n+1)}{2}$なので,整理すると
を得る.
4乗和・5乗和・……の公式の導出
2乗和の公式の導出と3乗和の公式の導出の違いは
- 等式$k^3-(k-1)^3=3k^2-3k+1$を使うか
- 等式$k^4-(k-1)^4=4k^3-6k^2+4k-1$を使うか
というだけですね.
2乗和・3乗和の公式と同様に
を考えることで,4乗和・5乗和,……の公式が順次得られます.
例えば,4乗和・5乗和は次のようになります.
等式
が成り立つ.
$m$乗和の公式($m=4,5,\dots$)が高校数学で使われることはほとんどありませんが,導出法は次の記事で扱う階差数列の公式に通ずるものがあるので知っておきましょう.
興味がある人は腕試しに導出してみてください.
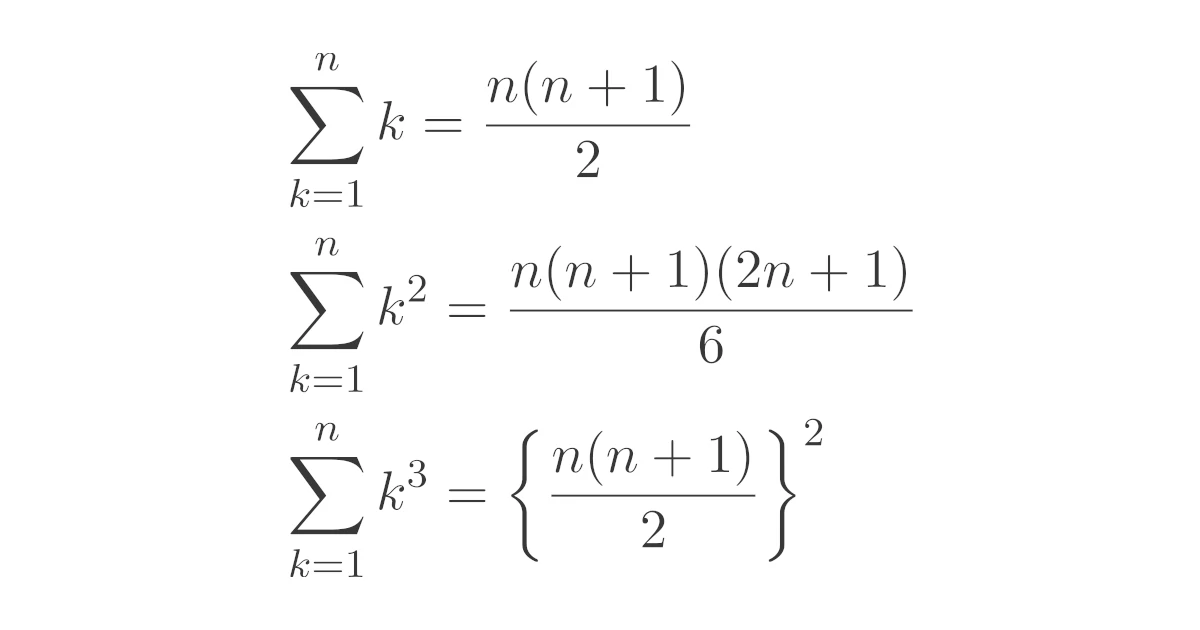
コメント