2次関数$y=ax^2$は
- $a>0$のとき,頂点$(0,0)$の下に凸な放物線を$xy$平面上に描き,$y$の最小値は0となる
- $a<0$のとき,頂点$(0,0)$の上に凸な放物線を$xy$平面上に描き,$y$の最大値は0となる
のでした.実は,1次の項$bx$と定数項$c$を加えた2次関数\begin{align*}y=ax^2+bx+c\end{align*}の$xy$平面上のグラフも放物線となり,平方完成という変形により頂点を求めることができます.さらに,その副産物として,$a>0$のときは$y$の最小値を,$a<0$のときは$y$の最大値を求めることができます.
この記事では
- 平方完成と2次関数のグラフ
- 平方完成の手順と具体例
- 2次関数のグラフと最大値・最小値
を順に解説します.
「多項式」の一連の記事
平方完成と2次関数のグラフ
まずは2次式の平方完成がどういうものか説明し,それをもとに2次関数$y=ax^2+bx+c$の頂点の求め方を説明します.
平方完成とは変数を2乗でまとめる変形のこと
例えば,2次式$x^2+2x-2$を考えます.2次式の2乗型の因数分解公式$x^2+2ax+a^2=(x+a)^2$より
\begin{align*}x^2+2x+1=(x+1)^2\end{align*}
ですから,
\begin{align*}x^2+2x-2=(x^2+2x+1)-3=(x+1)^2-3\end{align*}
と変形できますね.このように,変数を2乗にまとめる変形を平方完成といいます.
2次式$ax^2+bx+c$($a\neq0$)を
\begin{align*}a(x+\alpha)^2+\beta\end{align*}
の形の式に変形することを平方完成という.
2次関数を平方完成して頂点を求める
上でみた平方完成より,2次関数$y=x^2+2x-2$は
\begin{align*}y=(x+1)^2-3\end{align*}
と変形することができます.一般に実数の2乗は0以上ですから$(x+1)^2\geqq0$なので,$y\geqq-3$と分かります.また,$x=-1$のときに$y=-3$となります.
このことから,2次関数$y=x^2+2x-2$の$xy$平面上のグラフは下図のようなグラフになりそうですね.
実はこのグラフは放物線となっており,一般に2次関数$y=a(x-p)^2+q$($a\neq0$)は
- $a>0$のとき,頂点$(p,q)$の下に凸な放物線を$xy$平面上に描き,$y$の最小値は$q$
- $a<0$のとき,頂点$(p,q)$の上に凸な放物線を$xy$平面上に描き,$y$の最大値は$q$
となります.
いまの議論だけでは,グラフが放物線になることまでは言えていませんが,放物線となることはこの記事の最後で証明します.
平方完成の手順と具体例
一般に2次式$x^2+bx+c$の平方完成は次の手順によりできます.
- $b$の$\frac{1}{2}$倍の2乗$\bra{b\times\frac{1}{2}}^2=\frac{b^2}{4}$を足し引きする:$x^2+bx+\frac{b^2}{4}-\frac{b^2}{4}+c$
- $x^2+bx+\frac{b^2}{4}$を( )でひとまとめにする:$\bra{x^2+bx+\frac{b^2}{4}}-\frac{b^2}{4}+c$
- ( )の部分に2乗の因数分解公式を用いる:$\bra{x+\frac{b}{2}}^2-\frac{b^2}{4}+c$
一般的に書くと難しく感じるかもしれませんが,以下で具体的にやってみれば,それほど難しいものではないことが分かります.
具体例1($x^2+2x$の平方完成)
2次式$x^2+2x$を平方完成せよ.
$x^2+2x$の1次の係数2の$\frac{1}{2}$倍の2乗は$\bra{2\times\frac{1}{2}}^2=1$なので,この1を足し引きして
\begin{align*}x^2+2x&=x^2+2x+1-1\\&=(x^2+2x+1)-1\end{align*}
とします.このとき$x^2+2x+1$に2乗の因数分解公式が使えて
\begin{align*}x^2+2x=(x+1)^2-1\end{align*}
となります.
具体例2($x^2+6x+1$の平方完成)
2次式$x^2+6x+1$を平方完成せよ.
$x^2+6x+1$の1次の係数6の$\frac{1}{2}$倍の2乗は$\bra{6\times\frac{1}{2}}^2=9$なので,この9を足し引きして
\begin{align*}x^2+6x+1&=x^2+6x+9-9+1\\&=(x^2+6x+9)-9+1\end{align*}
とします.このとき$x^2+6x+9$に2乗の因数分解公式が使えて
\begin{align*}x^2+6x+1=(x+3)^2-8\end{align*}
となります.
具体例3(${}3x^2-6x+1$の平方完成)
2次式$3x^2-6x+1$を平方完成せよ.
2次の係数が1でない場合は,最初に2次の係数3で1次と2次をくくることで平方完成ができます.
$3x^2-6x+1$の2次の係数3で1次と2次をくくって
\begin{align*}3x^2-6x+1=3(x^2-2x)+1\end{align*}
です.( )の中の1次の係数−2の$\frac{1}{2}$倍の2乗は$\bra{-2\times\frac{1}{2}}^2=1$なので,この1を( )の中で足し引きして
\begin{align*}3x^2-6x+1&=3(x^2-2x+1-1)+1\\&=3\{(x^2-2x+1)-1\}+1\end{align*}
とします.このとき$x^2-2x+1$に2乗の因数分解公式が使えて
\begin{align*}3x^2-6x+1&=3\{(x-1)^2-1\}+1\\&=3(x-1)^2-3+1\\&=3(x-1)^2-2\end{align*}
となります.
具体例4(${}2x^2-2x+1$の平方完成)
2次式$2x^2-2x+1$を平方完成せよ.
この問題も2次の係数が2なので,最初にこの2で1次と2次をくくります.
$2x^2-2x+1$の2次の係数2で1次と2次をくくって
\begin{align*}2x^2-2x+1=2(x^2-x)+1\end{align*}
です.( )の中の1次の係数−1の$\frac{1}{2}$倍の2乗は$\bra{-1\times\frac{1}{2}}^2=\frac{1}{4}$なので,この$\frac{1}{4}$を( )の中で足し引きして
\begin{align*}2x^2-2x+1&=2\bra{x^2-x+\frac{1}{4}-\frac{1}{4}}+1\\&=2\brb{\bra{x^2-x+\frac{1}{4}}-\frac{1}{4}}+1\end{align*}
とします.このとき$x^2-x+\frac{1}{4}$に2乗の因数分解公式が使えて
\begin{align*}2x^2-2x+1&=2\brb{\bra{x-\frac{1}{2}}^2-\frac{1}{4}}+1\\&=2\bra{x-\frac{1}{2}}^2-\frac{1}{2}+1\\&=2\bra{x-\frac{1}{2}}^2+\frac{1}{2}\end{align*}
となります.
分数が現れても同じようにできますね.
2次関数のグラフと最大値・最小値
最初に具体的に2次関数$y=x^2+2x-2$で考えたように,一般の2次関数$y=ax^2+bx+c$($a\neq0$)の$xy$平面上のグラフを考えましょう.
2次関数のグラフは放物線
上でも説明したように,一般の2次関数$y=ax^2+bx+c$($a\neq0$)の$xy$平面上のグラフが放物線のグラフとなることを証明しましょう.
2次関数$y=a(x-p)^2+q$の$xy$平面上のグラフは
- $a>0$のとき,頂点$(p,q)$の下に凸な放物線
- $a<0$のとき,頂点$(p,q)$の上に凸な放物線
である.
$X=x-p$, $Y=y-q$とおくと$y=a(x-p)^2+q$は$Y=aX^2$となる.よって,$Y=aX^2$のグラフは$XY$平面上の放物線である.
$x=X+p$, $y=Y+q$なので,$Y=aX^2$のグラフを
- $X$軸方向にちょうど$+p$
- $Y$軸方向にちょうど$+q$
平行移動したグラフが$y=a(x-p)^2+q$のグラフなので,点$(p,q)$を頂点とする放物線である.
この証明からも分かるように,2次関数$y=ax^2+bx+c$のグラフは$y=ax^2$を平行移動してできる放物線ですね.
同様の議論により,一般に$y=f(x-p)+q$のグラフは,$y=f(x)$のグラフを$x$軸方向にちょうど$+p$,$y$軸方向にちょうど$+q$平行移動したものになります.図形と方程式の分野の記事で詳しく説明しています.
2次関数のグラフと最大値・最小値の具体例
2次関数のグラフを描くことができるということは,2次関数の最小値・最大値もグラフから読み取ることができるということになります.
以下の2次関数の$xy$平面上のグラフを描き,[ ]の中のものを求めよ.
- $y=x^2-2x+2$[最小値]
- $y=-\dfrac{1}{2}x^2-x$[最大値]
(1)の解答
平方完成により$y=x^2-2x+2$は$y=(x-1)^2+1$と変形できるので,グラフは頂点$(1,1)$の下に凸な放物線となる.
よって,($x=1$のときに)最小値$y=1$をとる.
(2)の解答
平方完成により$y=-\dfrac{1}{2}x^2-x$は$y=-\dfrac{1}{2}(x+1)^2+\frac{1}{2}$と変形できるので,グラフは頂点$\bra{-1,\dfrac{1}{2}}$の上に凸な放物線となる.
よって,($x=-1$のときに)最大値$y=\dfrac{1}{2}$をとる.
このように,2次関数の最大値・最小値を考える際には,平方完成からグラフを描いて考えると分かりやすいですね.
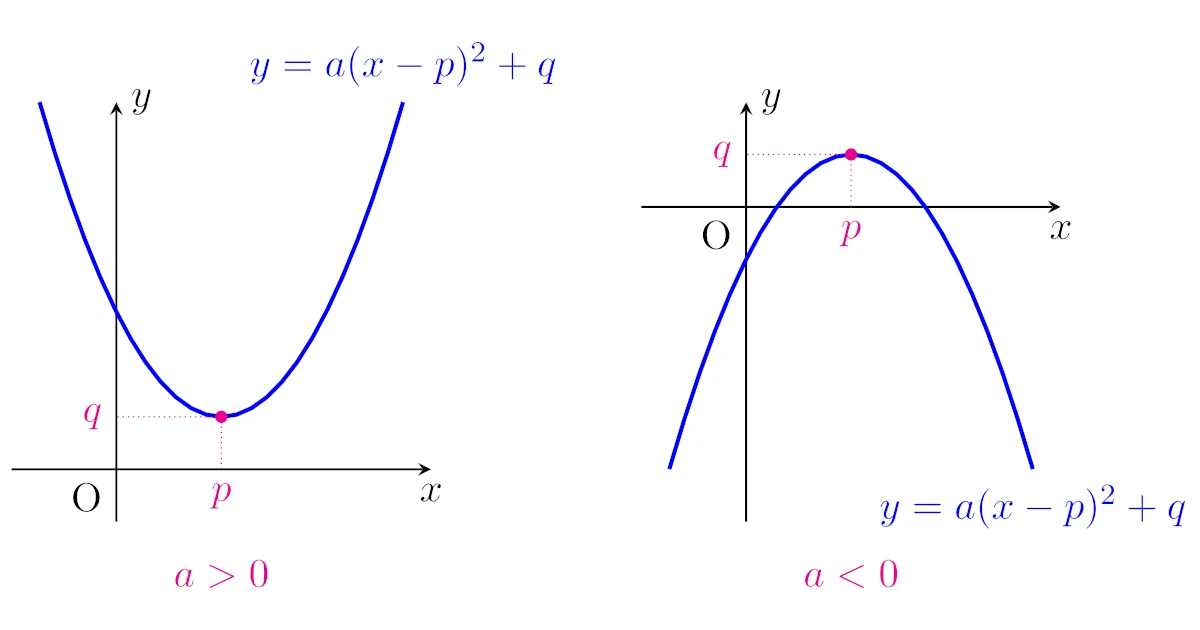
コメント