複素数を「見て」直感的に理解！複素平面と絶対値の考え方

前回の記事では，

$2$乗して$-1$になる数を虚数単位$i$
$a$, $b$を用いて，$a+bi$と表される数を複素数

と定義しましたが，これだと直感的なイメージが掴みづらいですね．

実数が数直線上に図示できるように，実は複素数は平面上の点として表すことができます．

この複素数を表す平面を複素平面といい，複素平面を用いることで複素数は視覚的に理解できるようになります．

この記事では

複素平面の考え方
複素数の絶対値

を具体例を用いて順に説明します．

「複素数」の一連の記事

複素平面
絶対値

複素平面

まずは複素平面の考え方から説明します．

複素平面の定義

ざっくり言えば，複素数$a+bi$と$xy$平面上の座標$(a,b)$とみなして表しすもので，以下のように定義されます．

$a$, $b$を実数とする．複素数$a+bi$を$xy$平面上の$(a,b)$と同一視して表す平面を複素平面（または複素数平面，ガウス平面）という．複素平面では，$x$軸に対応する軸を実軸，$y$軸に対応する軸を虚軸という．

異なる複素数が同じ点を表すことはありませんし，異なる点が同じ複素数を表すこともありませんから，複素数と複素平面上の点は１つ１つがピッタリ対応していますね．

具体例

複素数$1+i$, $3+2i$, $-\dfrac{3}{2}-2i$, $2-i$が表す複素平面上の点を図示せよ．

以下のようになる．

軸の“$\mrm{Re}$”を「実」と書いたり，“$\mrm{Im}$”を「虚」と書くこともあります．

また，$xy$平面上の点$\mrm{P}$が座標$(x,y)$を表すときに点$\mrm{P}(x,y)$と書くように，複素平面上の点$\mrm{P}$が複素数$z$を表すとき点$\mrm{P}(z)$と表します．

本来，点と複素数は異なるものですが，複素平面上のすべての点は複素数と対応するので，「複素数$z$を表す点」を「点$z$」ということも多いです．

対称移動

$a$, $b$を実数とする．複素数$z=a+bi$が表す複素平面上の点$\mrm{P}(z)$に対して，

$z$の$-1$倍$-z=-a-bi$
$z$の共役複素数$\overline{z}=a-bi$
$z$の$-1$倍の共役複素数$-\overline{z}=-a+bi$

が表す点をそれぞれ$\mrm{Q}_1(-z)$, $\mrm{Q}_2(\overline{z})$, $\mrm{Q}_3(-\overline{z})$とするとき，下図のようになりますね．

つまり，

点$\mrm{Q}_1(-z)$は点$\mrm{P}$と原点対称
点$\mrm{Q}_2(\overline{z})$は点$\mrm{P}$と実軸対称
点$\mrm{Q}_3(-\overline{z})$は点$\mrm{P}$と虚軸対称

となりますね．

絶対値

実数には絶対値がありましたが，複素数でも絶対値を考えることができます．

絶対値の定義

実数の場合の絶対値の定義は次の通りでした．

[実数の絶対値]　実数$x$に対して，数直線上の$0$と点$x$の距離を$x$の絶対値といい，$|x|$で表す．

このとき，絶対値の性質として

$\begin{align*}|x|=\begin{cases}x&(x\geqq0)\\-x&(x<0)\end{cases}\end{align*}$

は成り立ちますが，こちらは定義ではないので注意してください．

ワンポイント数学２
絶対値の定義から一瞬で解ける問題

絶対値を定義をきちんとイメージで理解していれば，不等式|x-3|<5や方程式|x-2|+|x-4|=8などはものの数秒で答えを出すことができます．この記事では，絶対値の定義を基礎から解説し，一瞬で解ける問題の考え方も紹介しています．

実数の絶対値と同様に複素数の絶対値は以下のように定義されます．

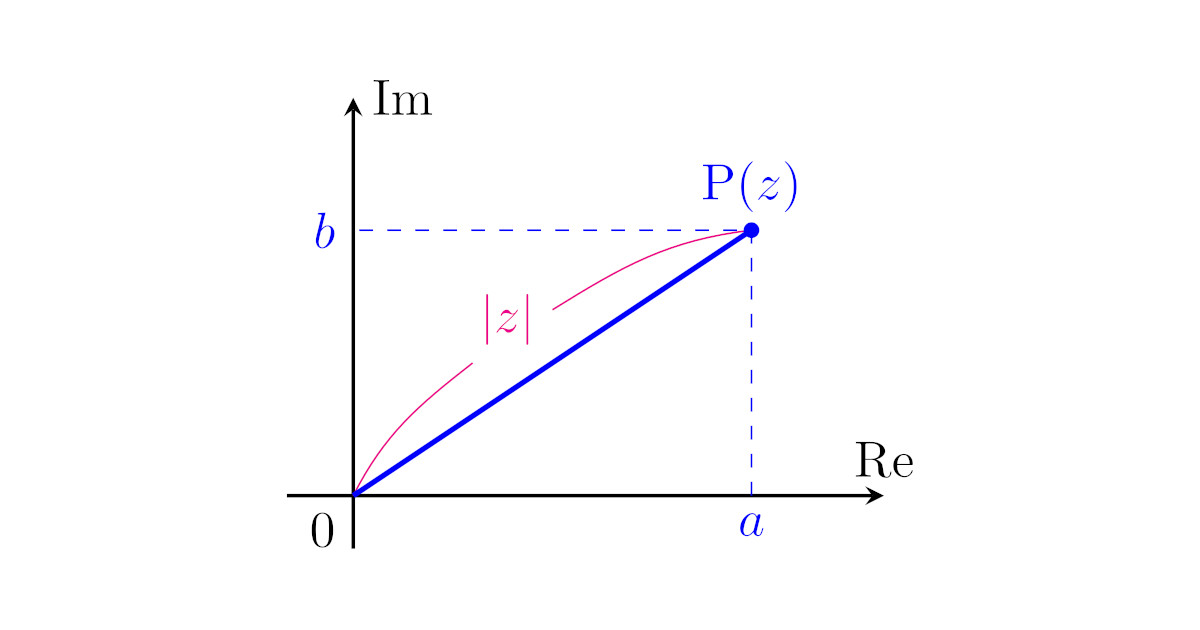
[複素数の絶対値]　複素数$z$に対して，複素平面上の$0$と点$z$の距離を$z$の絶対値といい，$|z|$で表す．

実数も複素数も絶対値といえば，原点との距離のことをいうわけですね．

絶対値の計算

それでは，複素数$z$の絶対値$|z|$がどのように計算できるのか考えましょう．

$z=a+bi$($a$, $b$は実数)と表すとき，複素平面上の点$\mrm{P}(z)$と原点$0$の距離は三平方の定理より$\sqrt{a^2+b^2}$ですから，

$\begin{align*}|a+bi|^2=a^2+b^2\iff|a+bi|=\sqrt{a^2+b^2}\end{align*}$

ということになりますね．

いま，

$\begin{align*}a^2+b^2=a^2-(bi)^2=(a+bi)(a-bi)\end{align*}$

ですね．$z=a+bi$より$\overline{z}=a-bi$なので，結局

$\begin{align*}a^2+b^2=z\overline{z}\end{align*}$

が成り立ちます．

ということで，以上をまとめた次を当たり前にしておきましょう．

複素数$z=a+bi$ ($a$, $b$は実数)に対して，

$\begin{align*}|z|^2=a^2+b^2=z\overline{z}\end{align*}$

が成り立つ．

ここでの注意点としては，$x$が実数なら$|x|^2=x^2$が成り立ちますが，$z$が複素数なら$|z|^2$と$z^2$は必ずしも等しくないという点です．

つまり，$|z|^2=z\overline{z}$の一方で$z^2=zz$ですから，$|z|^2=z^2$となるには$z=\overline{z}$であることが必要十分ですね．

よって，$z$が実数でないとき（つまり，$z$が虚数のとき）は$z^2=|z|^2$となりますね．

積の絶対値

実数$a$, $b$に対して$|ab|=|a||b|$が成り立つように，これは複素数に対しても同様に成り立ちます．

複素数$z$, $w$に対して，$|zw|=|z||w|$が成り立つ．

$|zw|$, $|z||w|$はともに$0$以上なので，$|zw|^2=(|z||w|)^2$を示せば$|zw|=|z||w|$が成り立ちますね．

$\begin{align*} |zw|^2 =&zw\cdot\overline{zw} =z\overline{z}\cdot w\overline{w} \\=&|z|^2\cdot|w|^2 =(|z||w|)^2 \end{align*}$

なので，$|zw|=|z||w|$が従います．

よって，$|z^n|$にこの公式を繰り返し用いれば，

$\begin{align*} |z^n| =&|zz^{n-1}| =|z||z^{n-1}| \\=&|z||zz^{n-2}| =|z||z||z^{n-2}| \\=&\dots \\=&|z||z|\dots|z| =|z|^n \end{align*}$

となって，$|z^n|=|z|^n$が成り立つことも分かりますね

厳密には数学的帰納法から証明できますね．