図形と方程式３<br>直線の「傾き」の考え方と平行条件・垂直条件

前回の記事では「方程式が表すグラフ」について説明しました．

平面上の図形の中で直線が最も単純な図形の１つで，中学校で学ぶように１次関数$y=ax+b$のグラフは（傾きをもつ）直線になりますね．

２つの直線$y=ax+b$, $y=a’x+b’$があるとき，これらの傾きに注目すると，これら２直線が平行か垂直かを判定することができます．

この記事では

傾きをもつ直線
傾きをもつ直線の平行条件・垂直条件

を順に説明します．

「図形と方程式」の一連の記事

傾きをもつ直線
1. 直線の傾き
2. 傾きをもつ直線の方程式
傾きをもつ直線の平行条件・垂直条件
1. 具体例
2. 証明

傾きをもつ直線

まずは傾きをもつ直線について，基本事項をまとめます．

直線の傾き

$xy$平面上の直線の傾きは以下のように定義されるのでした．

$xy$平面上の２点$\mrm{A}(x_1,y_1)$, $\mrm{B}(x_2,y_2)$について，$x_1\neq x_2$とする．このとき，

$\begin{align*}\frac{y_2-y_1}{x_2-x_1}\end{align*}$

を直線$\mrm{AB}$の傾きまたは変化の割合という．

$x_1\neq x_2$ということから点$\mrm{A}$の$x$座標と点$\mrm{B}$の$x$座標が異なるので，直線$\mrm{AB}$は$y$軸に平行でないときに直線の傾きが定義されるわけですね．

$x_1=x_2$なら$\dfrac{y_2-y_1}{x_2-x_1}$の分母が$0$になって定義できないので，$x_1\neq x_2$の場合で定義するわけですね．

$\dfrac{y_2-y_1}{x_2-x_1}$について，

$x_2-x_1$は点$\mrm{A}$から点$\mrm{B}$への$x$の変化量
$y_2-y_1$は点$\mrm{A}$から点$\mrm{B}$への$y$の変化量

を表すので，これらの比率が変わると直線の伸びる方向が変わるので，$\dfrac{y_2-y_1}{x_2-x_1}$を「傾き」や「変化の割合」というわけですね．

傾きをもつ直線の方程式

傾きをもつ直線の方程式は

通る点
傾き

の２つさえ分かれば，次で求めることができます．

$xy$平面上の点$(a,b)$を通り，傾き$m$の直線$\ell$の方程式は

$\begin{align*}y=m(x-a)+b\end{align*}$

である．

原点を通り傾き$m$の直線$y=mx$を

$x$軸方向にちょうど$+a$
$y$軸方向にちょうど$+b$

だけ平行移動すれば，点$(a,b)$を通り，傾き$m$の直線$\ell$となる．

よって，求める方程式は

$\begin{align*}&y-b=m(x-a) \\\iff&y=m(x-a)+b\end{align*}$

である．

グラフの平行移動について詳しくは前回の記事を参照してください．

xy平面上の「グラフ」とは？｜x,yの「方程式」を図示したい

y=2x+1やy=-x+3のようなx,yの等式はxy平面上の直線を表すように，一般にx,yの等式はxy平面上のグラフを表します．この記事では，「方程式が表すグラフ」「グラフの平行移動」を順に説明します．

今の考え方が分かれば一瞬ですが，以下のように計算で示すこともできます．

傾き$m$をもつ直線なので方程式は$y=mx+c$ ($c$は実数)と表せます．この直線が点$(a,b)$を通ることから，

$\begin{align*}b=ma+c\iff c=b-ma\end{align*}$

と$c$が求まり，求める方程式は

$\begin{align*}&y=mx+(b-ma) \\\iff&y=m(x-a)+b\end{align*}$

と得られますね．

傾きをもつ直線の平行条件・垂直条件

直線の傾きを比較することで２つの直線が平行か垂直かを判定することができます．

[平行条件・垂直条件]　$xy$平面上の傾き$m_1$をもつ直線$\ell_1$，傾き$m_2$をもつ$\ell_2$に対して，次が成り立つ．

$\ell_1$と$\ell_2$は平行である $\iff m_1=m_2$
$\ell_1$と$\ell_2$は垂直である $\iff m_1m_2=-1$

垂直条件$m_1m_2=-1$は$m_1=-\dfrac{1}{m_2}$とも書けることから，直線の傾きを逆数にして$(-1)$倍すれば垂直な直線の傾きとなりますね．

具体例

証明はひとまず後回しにして，具体的に問題を解いてみましょう．

$xy$平面上の次の直線の方程式を求めよ．

直線$y=2x-3$に平行で，点$(2,-1)$を通る直線$\ell_1$
直線$y=x-2$に垂直で，点$(0,1)$を通る直線$\ell_2$
直線$y=-2x+1$に垂直で，点$(1,1)$を通る直線$\ell_3$

(1)　直線$y=2x-3$に平行だから直線$\ell_1$の傾きも$2$で，点$(2,-1)$を通ることから，直線$\ell_1$の方程式は

$\begin{align*}&y=2(x-2)+(-1) \\\iff&y=2x-5\end{align*}$

となる．

(2)　直線$y=x-2$に垂直だから直線$\ell_2$の傾きは$-1$で，点$(0,1)$を通ることから，直線$\ell_2$の方程式は

$\begin{align*}&y=(-1)(x-0)+1 \\\iff&y=-x+1\end{align*}$

となる．

(3)　直線$y=-2x+1$に垂直だから直線$\ell_3$の傾きは$\dfrac{1}{2}$で，点$(1,1)$を通ることから，直線$\ell_3$の方程式は

$\begin{align*}&y=\frac{1}{2}(x-1)+1 \\\iff&y=\frac{1}{2}x+\frac{1}{2}\end{align*}$

となる．

証明

それでは証明しましょう．

[平行条件・垂直条件（再掲）]　$xy$平面上の傾き$m_1$をもつ直線$\ell_1$，傾き$m_2$をもつ$\ell_2$に対して，次が成り立つ．

$\ell_1$と$\ell_2$は平行である $\iff m_1=m_2$
$\ell_1$と$\ell_2$は垂直である $\iff m_1m_2=-1$

両方の向き($p\Ra q$, $p\La q$)が証明できて初めて，同値($p\iff q$)と言えることに注意しましょう．

同値（必要十分条件）については以下の記事を参照してください．

論理と集合３
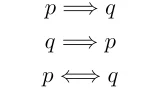
必要条件・十分条件を判断する１つのポイント

数学においては「pならばqである」という形の命題がよく登場します．この記事では，論理の基本として必要条件・十分条件がどういうものか説明し，具体的から判断するときのポイントを説明しています．

[平行条件]　下図のように，２直線$\ell_1$, $\ell_2$の切片より小さい切片をもち$x$軸に平行な直線$L$をとり，５点$\mrm{A}$, $\mrm{B}$, $\mrm{C}$, $\mrm{D}$, $\mrm{E}$をとる．

$\tri{ACE}$と$\tri{BCD}$は相似だから，

$\begin{align*}\frac{\mrm{CE}}{\mrm{AC}}=\frac{\mrm{CD}}{\mrm{BC}} \iff m_1=m_2\end{align*}$

が成り立つ．

一方$m_1=m_2$ならいまの議論を逆にたどることができて$\ell_1$と$\ell_2$が平行となる．

[垂直条件]　$m_1$, $m_2$の正負が等しければ垂直になり得ない．以下$m_2<0<m_1$で示す．

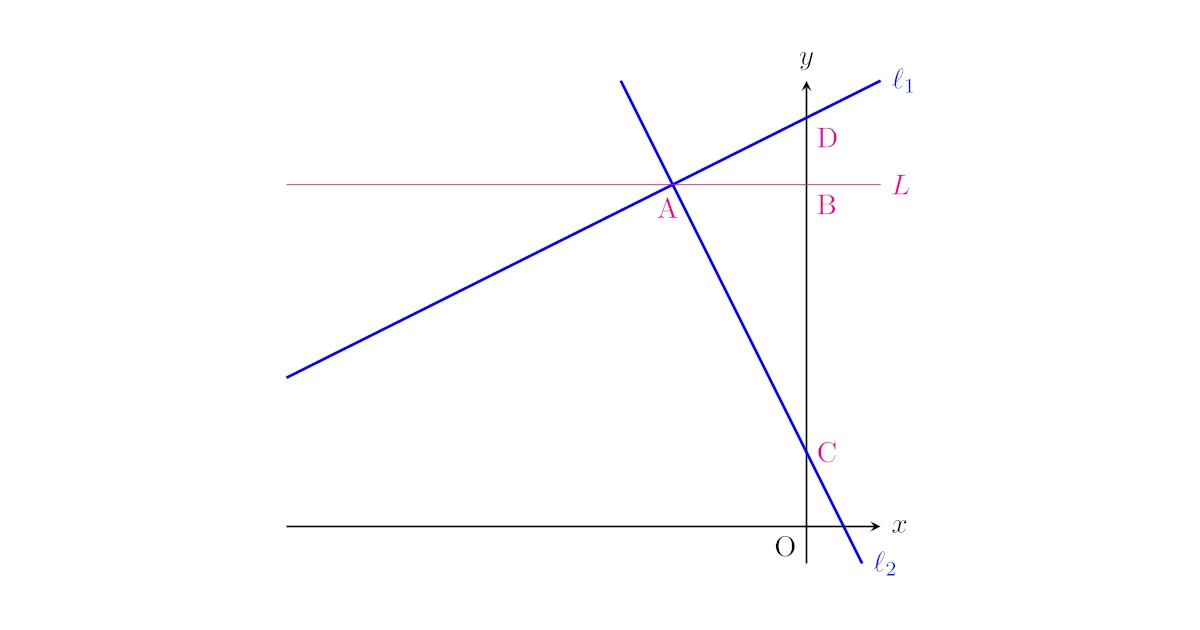
下図のように，２直線の交点を通り$x$軸に平行な直線$L$をとり，４点$\mrm{A}$, $\mrm{B}$, $\mrm{C}$, $\mrm{D}$をとる．

$\tri{ABC}$と$\tri{DBA}$は相似なので，

$\begin{align*}\frac{\mrm{BC}}{\mrm{AB}}=\frac{\mrm{BA}}{\mrm{DB}} \iff&\frac{-\mrm{BC}}{\mrm{AB}}\cdot\frac{\mrm{DB}}{\mrm{BA}}=-1 \\\iff&m_1m_2=-1\end{align*}$

が成り立つ．

一方$m_1m_2=-1$ならいまの議論を逆にたどることができて$\ell_1$と$\ell_2$が垂直となる．

最後の「一方〜」の部分は逆向きも証明できることを述べているわけですね．

図形と方程式３
直線の「傾き」の考え方と平行条件・垂直条件

傾きをもつ直線

直線の傾き

傾きをもつ直線の方程式

傾きをもつ直線の平行条件・垂直条件

具体例

証明

コメント