 多項式
多項式 解と係数の関係の考え方!2次方程式も3次方程式も同じ!
2次方程式ax²+bx+c=0が解α,βをもつとき,解と係数の関係と呼ばれる等式α+β=-b/a, αβ=c/aが成り立ちます.この解と係数の関係は覚えている必要はなく,考え方が分かっていれば瞬時に導くことができます.
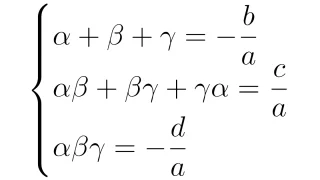 多項式
多項式  多項式
多項式  多項式
多項式  多項式
多項式  多項式
多項式  多項式
多項式  多項式
多項式  多項式
多項式  多項式
多項式  多項式
多項式