複素数は虚数単位$i$を用いて$a+bi$（$a$, $b$は実数）と表される数のことをいい，$a$を実部，$b$を虚部というのでした．
この実部と虚部で複素数を表す方法は，和や差を考える際には実部同士・虚部同士を計算すればよく簡単ですが，積や商はそれほど単純ではありません．
そこで，複素数の積や商の計算が簡単にできる複素数の表し方として極形式があります．
とくに$(a+bi)^n$など複素数の指数をこのまま計算しようとすると非常に面倒ですが，極形式の指数計算は非常に簡単で瞬時に答えが求まります．
この極形式の指数計算に関する定理をド・モアブルの定理といいます．ド・モアブルの定理はのちの記事で解説します．
この記事では
- 複素数の絶対値の復習
- 複素数の偏角
- 極形式の定義
- 極形式の具体例
を順に説明します．
「複素数」の一連の記事
絶対値と偏角
複素数の極形式を説明するには，絶対値と偏角をしっかり理解しておく必要があります．
絶対値
複素数の絶対値は前回の記事で説明したので，ここでは定義を確認しておきましょう．
複素数$z$に対して，複素平面上の$0$と点$z$の距離を$z$の絶対値といい，$|z|$で表す．
偏角
次に複素数の偏角について説明します．
偏角という言葉は三角関数を学んだ際にも出てきましたが，複素数の偏角も考え方は同じです．
複素平面上の原点$0$とは異なる点$\mrm{P}(z)$に対して，実軸の正方向からベクトル$\Ve{OP}$への有向角を(実軸正方向からの)複素数$z$の偏角という．ただし，反時計回りを正とする．
偏角は単なる角度とは異なり，「向きがある」ということに注意してください．
そのため，偏角は
- $360^{\circ}$を超えるもの
- 負のもの
も考えることができるわけですね．
極形式の考え方と定義
それでは本題の複素数の極形式を説明します．
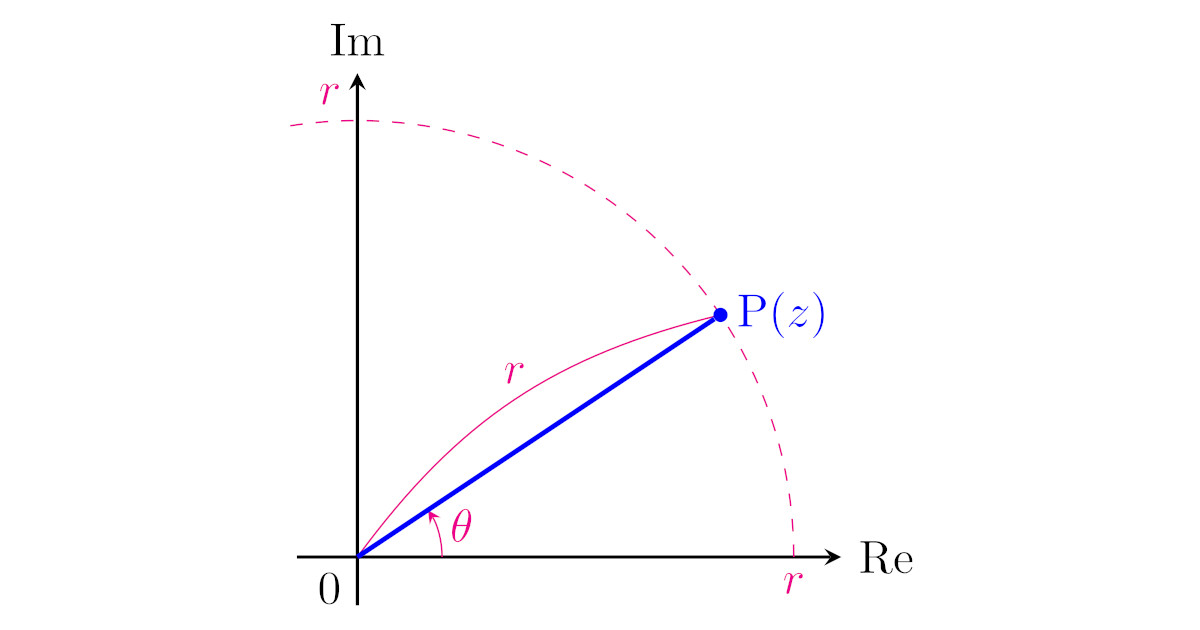
複素平面上に点$\mrm{P}(z)$をとったとき，どのように言えば点$\mrm{P}$の位置が相手に伝わるでしょうか？
１つは$z$の実部と虚部を考えて$z=a+bi$（$a,b$は実数）と表す方法ですね．
他に
- 点$\mrm{P}(z)$と原点$0$の距離$r$ ($r=|z|$)
- 点$\mrm{P}(z)$の偏角$\theta$
を指定することでも，点$\mrm{P}$の位置が分かりますね．
このとき，
- $z$の実部は$r\cos{\theta}$
- $z$の虚部は$r\sin{\theta}$
なので，
\begin{align*}z=r(\cos{\theta}+i\sin{\theta})\end{align*}
となることが分かりますね．この複素数の表し方を極形式と呼びます．
$r\geqq0$とし，$\theta$を実数とする．絶対値$r$，偏角$\theta$の複素数$z$の
\begin{align*}z=r(\cos{\theta}+i\sin{\theta})\end{align*}
という表し方を$z$の極形式という．
極形式の具体例
それでは複素数の極形式の具体例を考えましょう．複素数の絶対値が次で得られることを思い出しておきましょう．
複素数$z=a+bi$に対して，$|z|=\sqrt{a^2+b^2}$が成り立つ．
例１
複素数$z=\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}i$を極形式$z=r(\cos{\theta}+i\sin{\theta})$（$-\pi\le\theta<\pi$）に書き直せ．また，複素平面上に$z$が表す点$\mrm{P}(z)$を図示せよ．
$z=\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}i$の絶対値は
\begin{align*}|z|=\sqrt{\bra{\frac{1}{2}}^2+\biggl(\frac{\sqrt{3}}{2}\biggr)^2}=\sqrt{\frac{1+3}{4}}=1\end{align*}
である．よって，
\begin{align*}z=1\cdot\biggl(\frac{1}{2}+\frac{\sqrt{3}}{2}i\biggr)
=1\cdot\bra{\cos{\frac{\pi}{3}}+i\sin{\frac{\pi}{3}}}\end{align*}
が極形式である．よって，$z$の偏角が$\dfrac{\pi}{3}$と分かったから，複素平面上では下図のようになる．
例２
複素数$z=1-i$を極形式$z=r(\cos{\theta}+i\sin{\theta})$（$-\pi\le\theta<\pi$）に書き直せ．また，複素平面上に$z$が表す点$\mrm{P}(z)$を図示せよ．
$z=1-i$の絶対値は
\begin{align*}|z|=\sqrt{1^2+(-1)^2}=\sqrt{2}\end{align*}
である．よって，$\sqrt{2}$でくくって
\begin{align*}z&=\sqrt{2}\bra{\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}i}
\\&=\sqrt{2}\bra{\cos{\bra{-\frac{\pi}{4}}}+i\sin{\bra{-\frac{\pi}{4}}}}\end{align*}
が極形式である．よって，$z$の偏角が$-\dfrac{\pi}{4}$と分かったから，複素平面上では下図のようになる．
例３
複素数$z=-\sqrt{3}-3i$を極形式$z=r(\cos{\theta}+i\sin{\theta})$（$-\pi\le\theta<\pi$）に書き直せ．また，複素平面上に$z$が表す点$\mrm{P}(z)$を図示せよ．
$z=-\sqrt{3}-3i$の絶対値は
\begin{align*}|z|=\sqrt{(\sqrt{3})^2+(-3)^2}=\sqrt{12}=2\sqrt{3}\end{align*}
である．よって，$2\sqrt{3}$でくくって
\begin{align*}z&=2\sqrt{3}\biggl(-\frac{1}{2}-\frac{\sqrt{3}}{2}i\biggr)
\\&=2\sqrt{3}\bra{\cos{\bra{-\frac{2\pi}{3}}}+i\sin{\bra{-\frac{2\pi}{3}}}}\end{align*}
が極形式である．よって，$z$の偏角が$-\dfrac{2\pi}{3}$と分かったから，複素平面上では下図のようになる．
コメント